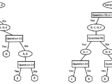Decision Trees for Watermark Identification in Rembrandt’s Etchings

Introduction

Incorporating watermark classification in studies of prints has been common practice for several centuries. As imaging technology continues to improve, higher-quality images reveal finer details of watermarks and offer more possibilities for their computational exploitation in print support analysis. In this article, suitably high-resolution scans of radiographs of prints by Rembrandt van Rijn (1606–1669) are processed to identify papers made on the same mold, which assists in dating the creation of the impressions. We exploit the decision-tree concept to build a tool for identifying watermarks in the paper supports of Rembrandt’s prints. This user-friendly tool can be used to find sheets of paper with the same watermark, and therefore made on the same mold. Our motivation can be explained by our agreement with Neil Harris’s claim that “If we can work backwards from the object made on the mould to establish the physical characteristics of the mould itself, and thus to relate it to other objects formed on the same mould, the outcome is an important tool for bibliographical research”¹ and Louisa Wood Ruby’s observation that “identifying watermarks has always been a laborious process.”² The decision-tree tool described here, with examples of its use and fabrication, is intended to make that process much less laborious.

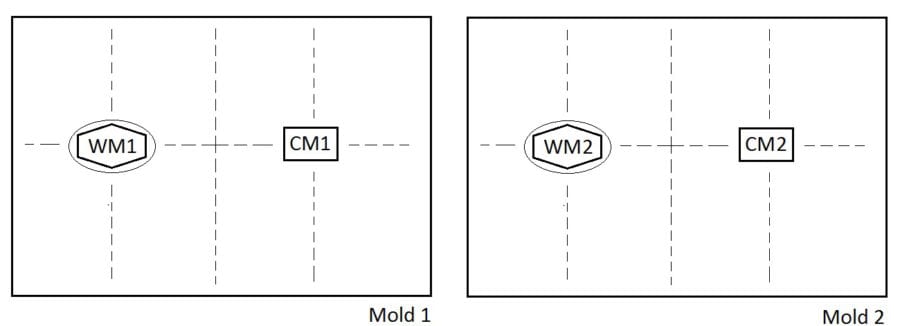
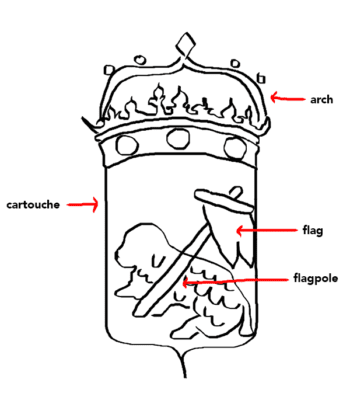
The wire watermark sits atop a screen of parallel wire lines laid close together (5 to 20 wires/cm). The watermark is tied down to this laid-line screen. The laid-line screen is supported by a perpendicular set of wire chain lines (spaced approximately 1 inch apart). This screen is anchored to a rectangular wooden frame, with parallel rods in the frame below the screen typically spanning the shorter dimension of the rectangular frame. The mold, i.e. the screen and frame combination,³ is dipped by the vatman into a vat of aqueous pulp. The vatman pulls the screen from the vat in a horizontal position and shakes it slightly to encourage the water to drain through the screen, leaving a sheet of paper of near-uniform thickness on the screen. The vatman hands the mold with the new sheet to the coucher, who presses and rotates the face of the mold against a piece of felt to clear the sheet from the screen. While the coucher removes the new sheet of paper from one screen, the vatman scoops pulp for the next sheet, using the second “twin” mold in a pair that were made together and equipped with nearly identical watermarks.⁴

A seventeenth-century European rectangular paper-making mold composed of a wooden rim surrounding a screen of (horizontal) closely-spaced laid lines and (vertical) further-apart chain lines can have a watermark centered in one half and a countermark centered in the other half. Countermarks are typically not as intricate as watermarks. In the two “twin” molds used to produce a batch of paper at a single vat, the two watermarks were made to be nearly identical. The countermarks were also made to match each other, but typically not as carefully. Sheets in a batch of paper made with a pair of molds illustrated in figure 1 might be cut in half or quarters or eighths before being sold. The resulting batchmates could have watermark 1, watermark 2, countermark 1, or countermark 2; or a fragment (for quartos and octavos) of any of these; or both watermark 1 and countermark 1 or both watermark 2 and countermark 2, in a single sheet. Due to the common practice, following Rembrandt’s death, of trimming prints to the edge of the plate mark, there is also the possibility that sheets may have no watermarks or fragments, which is common in quartos and octavos.

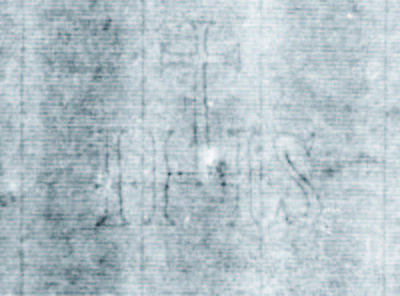
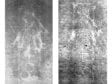
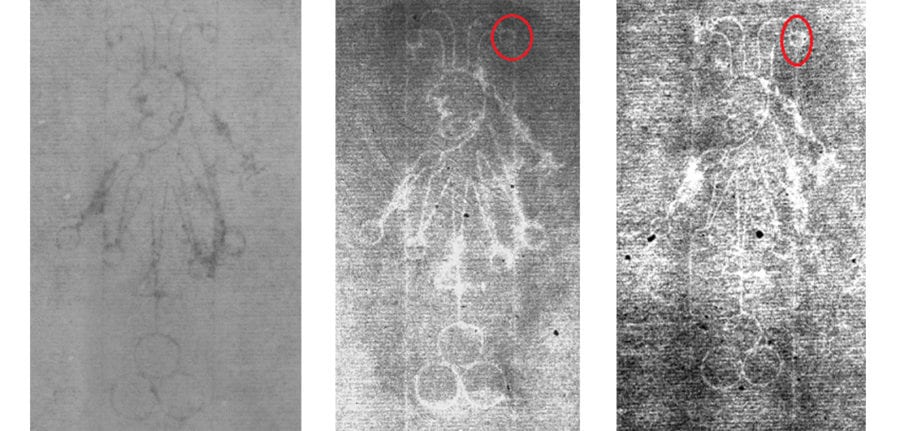
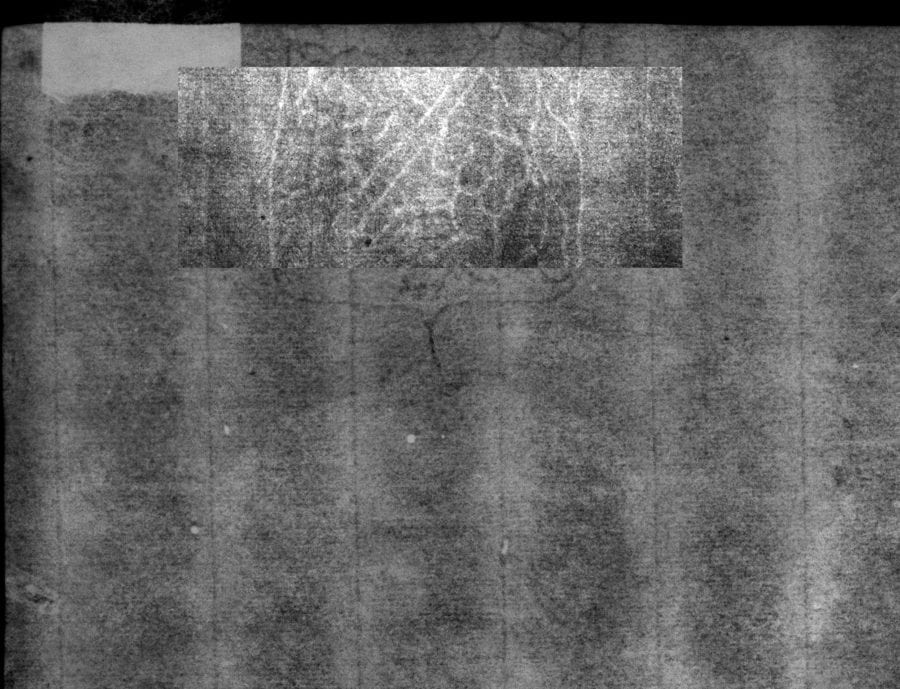
All three manufactured patterns—watermarks/countermarks, chain line spacings, and (less clearly) laid line density—are visible in a transmitted-light photo of a blank sheet of sixteenth-century French laid paper in figure 2. Here the reader will find all three pattern types (legible due to thinner, more transparent segments of the paper) with labels. Given the opaque ink in the printed surface image, a key portion of the watermark could be hidden in a transmitted light image. To address this problem, a commonly used imaging technology for the study of watermarks in antique laid paper is beta-radiography, which is unaffected by the thin ink layer but attenuated relative to the paper thickness.⁵ Figure 3 provides an example where, in the transmitted-light image, the surface art obscures the area just below the “IHS,” making a decision about possible features in that location impossible. A beta-radiograph reveals the full watermark and nearby chain lines and laid lines but does not include the artwork on the surface of the paper.⁶

Shortly before the end of the twentieth century, Nancy Ash and Shelley Fletcher provided a foundation for a hierarchical classification of the various watermarks in the European laid-paper supports of Rembrandt’s prints.⁷ This focus on the paper supports of work by a single artist is one reason that precise classification can be done visually. Watermark identification of a denser group, such as all artists in Amsterdam in the seventeenth century, would probably result in such a large database of watermarks that totally visual distinctions between separate batches would be practicably unfeasible. Another benefit of classifying the watermarks in Rembrandt’s prints is that these prints have been well studied. There are a variety of facts and opinions about various aspects, including dating, with which the watermark information can meld.

Ash and Fletcher’s test of an exact match relied on the ability to collect contact (exact-size) photographic images from beta-radiograph negatives for overlay comparison. A strong impetus for identifying a group of impressions from different plates on papers displaying the exact same watermark is the assistance such identification can provide in the dating of impression creations. For example, for impressions made on the same paper, the latest dated plate provides a date at or after which the paper must have been used. This is due to Rembrandt’s practice of reprinting plates at dates later than the date inscribed in the plate, along with more recently completed plates. For their study, Ash and Fletcher examined 2,765 impressions, of which only 936 (or approximately one-third) contained watermarks.

Erik Hinterding’s classification of the watermarks in Rembrandt’s prints used the hierarchical labeling foundation established by Ash and Fletcher.⁸ Hinterding examined more than 7,000 Rembrandt etchings, among which approximately one-third (2,369) had complete or fragmentary watermarks. He identified 1,998 of these marks and found 680 different ones, classified in fifty-four general types (Ash and Fletcher listed only thirty-nine), 294 variants across all of the types, and 512 subvariants (including twins). Hinterding estimates that Rembrandt used approximately 258 batches of paper. All papers with the watermark of a particular subvariant are batchmates, and their associated prints’ creation dates are all assumed to be from the same period.

Since 2012, we have been evaluating the uniqueness of chain line patterns in Rembrandt’s etchings.⁹ This was motivated by a desire to extend moldmate identification beyond the one-third of prints that possess legible watermarks. Our original image data came from the Morgan Library & Museum and the Metropolitan Museum of Art, both in New York. To increase the likelihood of moldmates, we needed access to a database of radiographs of Rembrandt’s prints from many collections. We were fortunate to be granted access to such an image dataset developed by the Dutch University Institute for Art History in Florence. This provided us with more than 700 full-print radiograph images of full watermarks. We had written software for marking and matching chain line patterns, but a problem remained: how would we confirm that prints with matching chainspace patterns were indeed moldmates? The obvious answer was to have previously identified all of the watermarks in our dataset. Then confirmation could be done quickly. But separately identifying the hundreds of watermarks in our dataset with confidence was considered far too time-consuming, given the close similarity of many of the watermarks, unless we could at the same time develop a procedure that could be used by future researchers to shorten significantly the time needed for watermark identification in Rembrandt’s etchings.

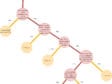
The WIRE (Watermark Identification in Rembrandt’s Etchings) Project was launched in 2015 to address this issue.¹⁰ The intent from the start was to involve students in the development of decision trees for all fifty-four watermark types in Hinterding’s catalogue. We began by imagining a computer-based interrogatory that at each step poses a yes/no question (or another “binary” question having two answers) to address the two possibilities for a particular feature. Each question is accompanied by two figures, one providing a sample for which the answer is “no,” and another for which the answer is “yes.”¹¹ The selection of “yes” or “no” will determine the next question. Questions will continue until the user reaches an endpoint of the decision tree. At that point, there will be no other watermark in Hinterding’s classification library that has the same sequence of yes/no answers to the questions the user has answered, and thus the given support will be identified. By 2018, we had developed many branches of the decision tree.

In 2018, just over one hundred years after Henry Clay Frick purchased eight prints by Rembrandt van Rijn on European laid paper, beta-radiographs revealed that seven of these prints had watermarks or watermark fragments. These seven prints, each accompanied by its beta-radiograph displaying the watermark (or a fragment), appear in figures 4–10.

The discovery of the watermarks prompted The Frick Collection to share the beta-radiographs with the WIRE Project, with the goal of using the decision trees being developed to identify the watermarks (and possibly even the fragments) in this latter group of objects. This research resulted in the following discoveries.

One print in The Frick Collection can be dated to a particular year in the seventeenth century by its watermark. The same print offers the first case in which an impression of this plate has been found bearing this watermark.

The watermark in another print suggests a different date than that adopted by The Frick Collection. The same print has a watermark appearing in impressions from nineteen different plates.

Two of the prints are on paper from the same batch.

One print is a portrait that was printed after the plate had been transferred to the sitter, yet it is on paper with the same watermark as that of the first state, which was printed by Rembrandt. This possibly indicates a closer interaction between Rembrandt and the patron than previously imagined.

The insights listed above were based on watermark identification performed in mere minutes, using a binary decision tree, once the branch for each corresponding watermark type had been constructed.

With further applications of the WIRE Project’s methods in mind, this article describes the decision tree branches used to identify the watermarks in the seven Frick Collection prints by Rembrandt. It aims to help guide the development of decision trees for rapid and confident identification of watermarks in works by other artists, and for rapid identification of a variety of other maker marks. Once we have described the mechanism supporting our watermark identifications, we can connect specific prints to the discoveries above.¹²

Watermark Identification using the Decision-Tree Format

The WIRE Project at Cornell uses a decision-tree format to accelerate the process of identifying watermarks in Rembrandt’s etchings according to Hinterding’s taxonomy. Such watermark identification can support the development of a chronology of Rembrandt’s print production, which is useful in analyzing Rembrandt’s artistic development and commercial activities.¹³

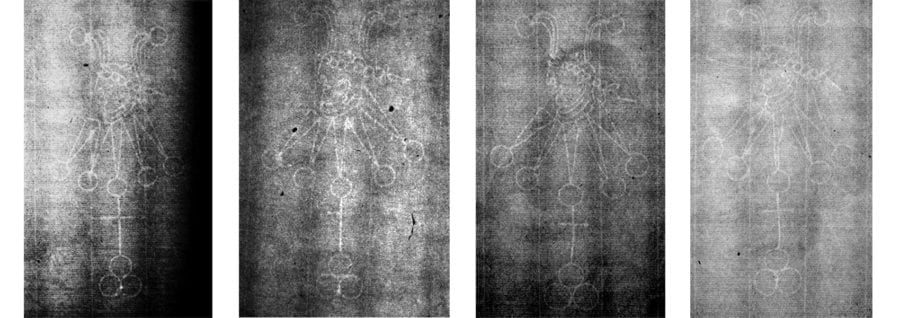
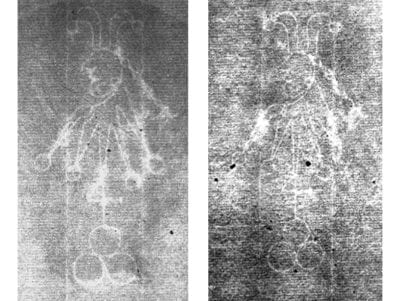
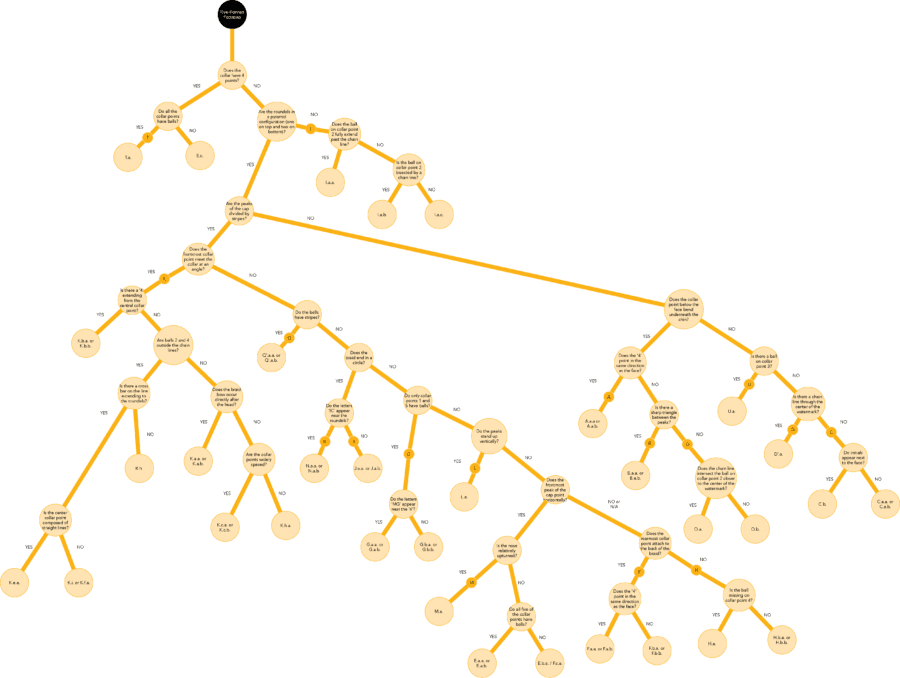
A difficulty with utilizing Hinterding’s hierarchical labeling to identify a specific watermark is the tediousness of searching through more than 500 possible matches, many of which are highly similar to one another. This is best demonstrated by an example: the Foolscap with Five-pointed Collar. Four of the eighteen variants of this type are illustrated in figure 11, and each variant has distinct subvariants, for a total of thirty.¹⁴ Four of these, all subvariants of variant K, are illustrated in figure 12. The four subvariants in figure 12 are more similar to one another than are the four variants in figure 11. Furthermore, within a subvariant category there can be highly similar twins, such as in figure 13. As can be inferred from the watermark labels in figures 11–13, the labeling convention is an uppercase letter for a particular variant, a first lowercase letter for a specific subvariant, and a second lowercase letter designating the specific twin. A watermark with a chain line down its middle is identified with an uppercase letter including an apostrophe as the variant label, e.g. A’.¹⁵ Highly similar twins arise due to the rotation of a pair of papermaking molds in a production process that is intended to produce a batch of paper with the “same” watermark.¹⁶ As one progresses deeper into the type/variant/subvariant/twin taxonomy, the differences become harder to recognize unless one knows which specific points to compare in the watermark images.

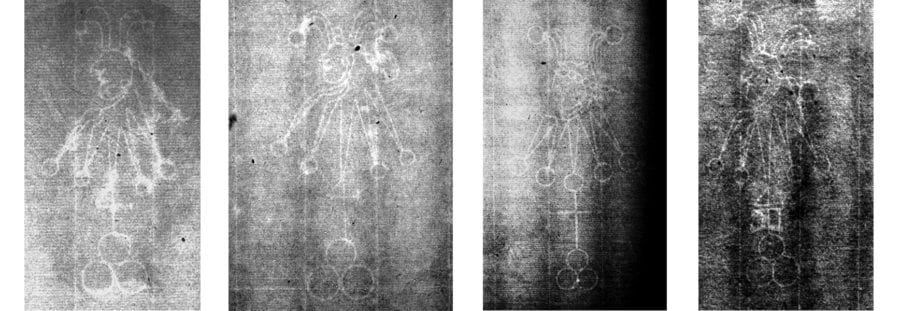
The decision-tree concept used here is similar to the parlor game of “Twenty Questions.” The category of “animals” provides a good example. Reasonable questions might include: “Can it fly?” “Does it have four legs?” “Does the mature version typically weigh less than one pound?” “Can it be found in North America?” If the answers pertained to a particular type of dog, the responses to these questions would be “no,” “yes,” “no,” and “yes.” The answer to each question shrinks the group of possible solutions. For example, the answer “no” to the first question eliminates most birds as a possibility. But, because many animals would satisfy all four answers, such as a cat, many more questions would be needed to arrive at the specific type and breed of the animal. Along the way, as one gets closer to the final answer the questions asked could depend on the answer to the preceding question(s). For example, if the answer to the first question were “yes” instead of “no,” the next question might not be about the number of legs but rather whether or not it has feathers.

Returning to the variants in figure 11, we can refine our identification by asking the following questions:

1.   Are there letters above the roundels?
2.   Are both bells on the peaks of the cap within the chain lines on either side of the face?
3.   Does the center collar point have a ball at its apex?

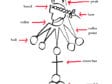
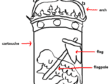
The first problem in answering these questions is one of terminology. For example, what are “roundels,” “bells,” “peaks,” “collar points,” “balls,” and “chain lines”? Refer to figure 14, which distinguishes the circles at the top as “bells,” those in the middle as “balls,” and those at the bottom as “roundels.”

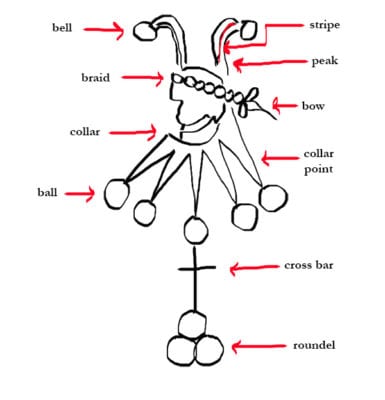
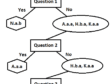
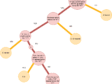
Once we resolve our terms, the answers to question 1 for the four watermarks in figure 11 are: far left, no; middle left, no; middle right, no; and far right, yes. Thus, question 1 separates the lower-right image for N.a.b from the others. If the watermark of interest was known to be one of these four choices, an affirmative answer to question 1 would end the search, with N.a.b as the answer. A negative answer leaves the three remaining choices. Asking question 2 of these three yields the following answers: top left, yes; top right, no; and bottom left, no. This separates A.a.a from the other two. Assuming that the answer for the watermark being identified is “no,” we proceed to ask question 3. The answers for the remaining two choices are: top right, no, bottom left, yes. If the answer for the watermark being identified is “yes,” this identifies the watermark of interest as K.a.a. This sequence of questions results in the decision tree in figure 15.

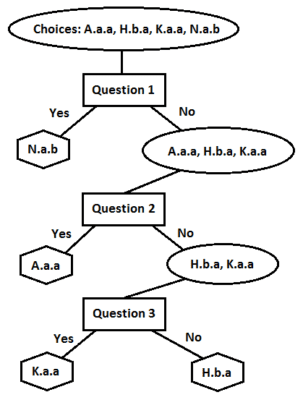
Another way to organize the information gained by answering the three questions in our example is as a decision table including binary yes/no answers to all questions for all possible classifications, as in Table 1 where yes = 1 and no = 0. The sequence of binary digits represents an identifying code for each watermark, with A.a.a identified by 010, H.b.a by 000, K.a.a by 001, and N.a.b by 100. Note that the four codes are different. Furthermore, each code has only one nonzero digit. This suggests that any ordering of the questions will result in a successful decision tree.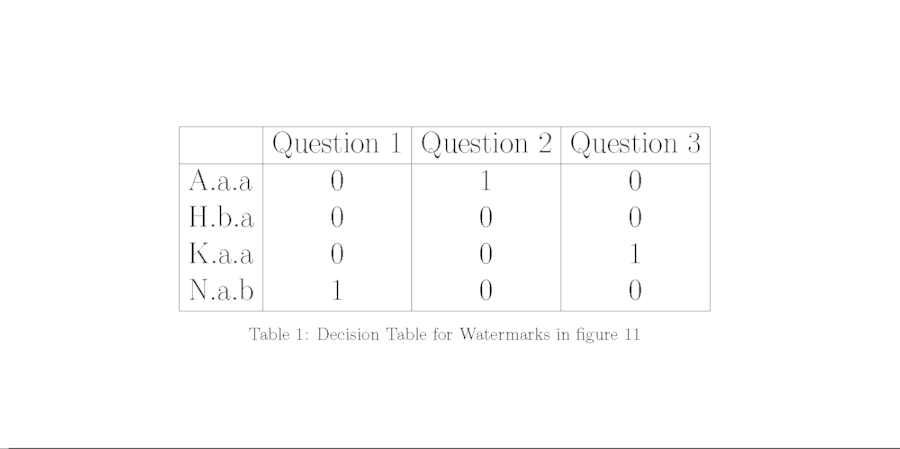

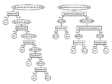
Selecting features around which to compose yes/no questions is the time-consuming portion of decision-tree construction. One key requirement of these questions is that they should be phrased in such a way that users can answer them with total confidence. This is best tested by vetting the candidate questions with a team rather than a single individual. The questions should not solicit an opinion but should query an obvious fact. Also important is the ability of the questions to accommodate images without regard to their scale. Re-scaling images to a common resolution requires accurate recordkeeping about their creation, including the particulars of their digitization. However, such records often are unavailable (or unreliable). Thus, only scale-invariant questions are used. For example, a question asking if a dimension of some element in the image is longer than, for example, 2 centimeters is unacceptable; the specified resolution in dots per inch may be imprecise or unavailable. Questions should focus on the relative size (e.g., is the distance between two specified points in the watermark greater than the distance between another pair of specified points), relative location (e.g., is one particular element of the watermark to the left or above another element of the watermark, which will require adherence to a specific orientation for evaluation of that watermark), relative orientation (e.g., is some element of the watermark tilted relative to a nearby chain line), or relative number (e.g., does a foolscap collar have four points). Following these guidelines, the WIRE Project team has produced the decision tree in figure 16 for all full-watermark occurrences of the Foolscap with Five-pointed Collar watermark in Rembrandt’s etchings in Hinterding’s catalogue.¹⁷

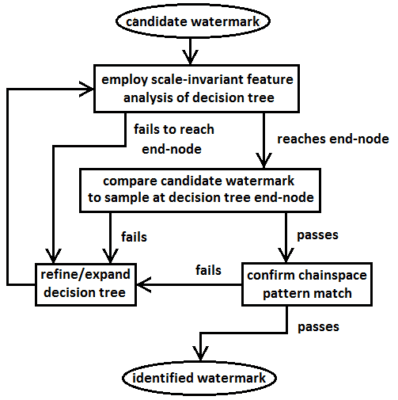
Sometimes the decision tree cannot be completed successfully because the watermark being identified is only a fragment of the full watermark, because the user erred when answering the decision-tree questions, or because the watermark being identified may not be in Hinterding’s catalogue. Thus, verification mechanisms are needed. To this end, we compare the watermark of interest to the image of the watermark in Hinterding’s catalogue that was identified as a match by the decision tree. We also check the match of the chainspace pattern in the print of interest to the reference print from Hinterding’s catalogue. In both instances the match should be exact.

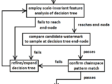
The first mechanism requires close looking.¹⁸ The second mechanism will probably require some adjustment in one of the two images, as they will often be digitized at different resolutions. Furthermore, prints that have been subject to different degrees and types of conservation may exhibit different amounts of shrinkage. While these shrinkage effects are typically modest, a small difference could lead to the failure of a visual overlay comparison.¹⁹ Fortunately, shrinkage appears to be largely uniform in the direction perpendicular to the chain lines. Thus, the chainspace comparison can be done by first re-scaling one image so the same pair of chain lines near the center of the watermark is matched in the two images, and then checking to see if the other chain lines in the two images are aligned. (The verification is more reliable for images including more chain lines.²⁰) Consequently, the flowchart for watermark identification in figure 17 has a feedback loop in case of a confirmation failure, through a refine/expand mode that leads the user back to the start of the identification procedure. Construction and use of the decision-tree-based watermark identification procedure is illustrated in the next section using the seven Rembrandt prints with watermarks in The Frick Collection.²¹ This study of the watermarks in The Frick Collection’s Rembrandt prints is the centerpiece of this paper.

The WIRE Project Examines the Frick Collection’s Rembrandt Prints

In July 2018, Margaret Holben Ellis (New York University) and Reba Fishman Snyder (The Morgan Library & Museum) took beta-radiographs of prints by Rembrandt in The Frick Collection. Lydia Aikenhead (New York University) stitched together the resulting images. Watermarks or watermark fragments appeared in radiographs of seven of the prints. These images were sent to the WIRE Project for analysis, using the decision trees under development. Watermark identification was successful for all seven prints.

Landscape with Three Trees

The Frick Collection’s impression of Rembrandt’s Landscape with Three Trees and its beta-radiograph appear in figure 4. The watermark appears near the left edge of the beta-radiograph. A close-up of the watermark appears in the left image in figure 18.

Five questions and answers form the path highlighted in figure 19, through the Foolscap with Five-pointed Collar decision tree in figure 16 to identification of the watermark in the left image in figure 18.

Questions and Answers Leading to Foolscap with Five-pointed Collar A.a
Does the collar have four points?									NO
Are the roundels in a pyramid configuration (one on top and two on bottom)?									YES
Are the peaks of the cap divided by stripes?									NO
Does the collar point below the face bend underneath the chin?									YES
Does the “4” point in the same direction as the face?									YES

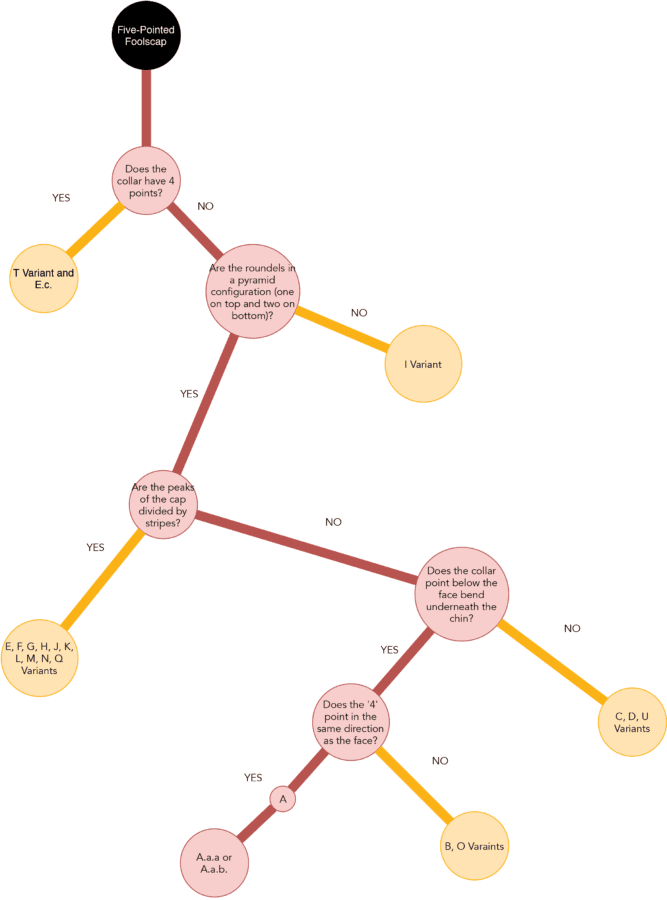
To help interpret the features cited in these questions, refer to the feature labels in figure 14. In the envisioned computer-based interrogatory, examples of “yes” and “no” answers to each of the questions would be provided, as in figures 20–24, to assist the user. This decision-tree path terminates with a designation of the subvariant as A.a

The Foolscap with Five-pointed Collar subvariant A.a has twins A.a.a and A.a.b illustrated in the middle and right images in figure 18. The twins A.a.a and A.a.b are very similar, but not identical. One distinction is that the bell on the right peak of A.a.b is bisected by a chain line, while the bell on the right peak of A.a.a is not. These bells are circled in red in figure 18. The corresponding bell in the watermark under investigation is not bisected by a chain line. Thus, the watermark comparison indicates that The Frick Collection’s Landscape with Three Trees has watermark A.a.a. This identification is supported by the chainspace pattern match in figure 25.

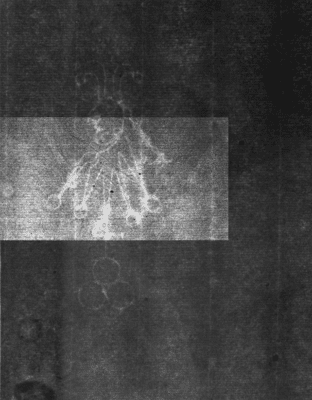
Hinterding cites six impressions of Landscape with Three Trees with this watermark (A.a.a), nine impressions of the same print with the twinmark (A.a.b), three impressions of the same print with an “unidentified twinmark,” and one as an “unverified reference.”²² Hinterding dates the prints in this batch (and thus The Frick Collection’s impression) to 1643 and cites ten prints with thirty-one impressions.²³ The Frick Collection’s impression expands the size of this batch to thirty-two impressions.

Jan (Johannes) Lutma the Elder

The Frick Collection’s impression of Rembrandt’s Jan (Johannes) Lutma the Elder and its beta-radiograph appear in figure 5. The watermark appears in the center of the beta-radiograph. A close-up of the Foolscap with Five-pointed Collar watermark appears on the left in figure 26.

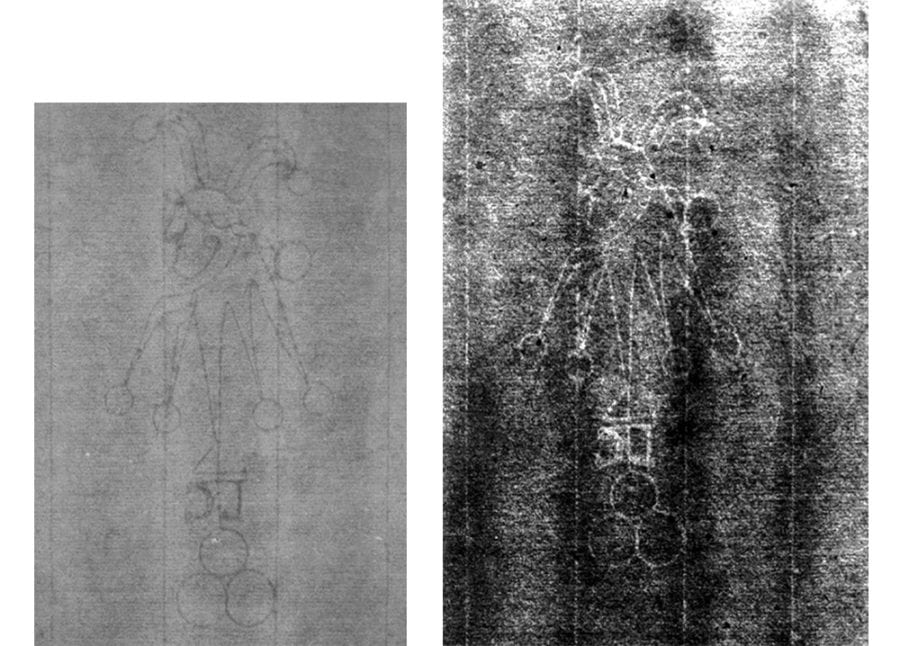
Seven questions and answers in the Foolscap with Five-pointed Collar decision tree in figure 16 identify the watermark under investigation in figure 26.

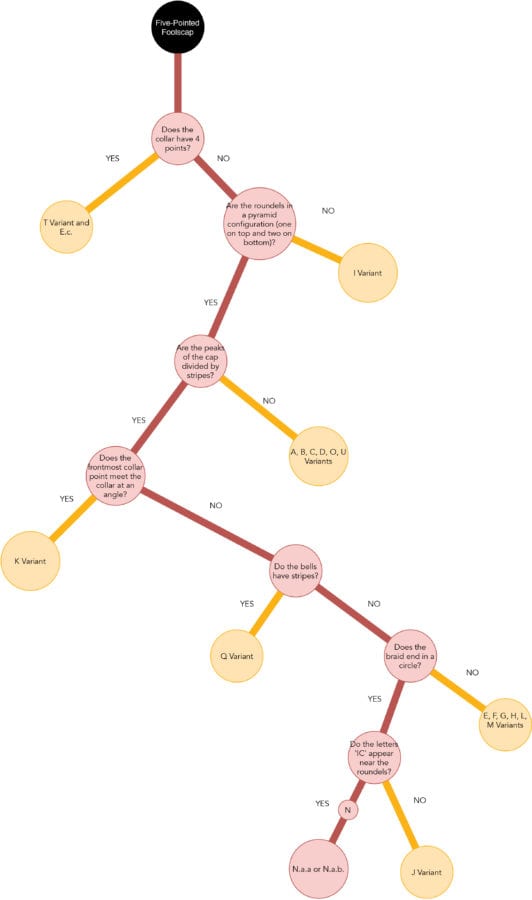
Questions and Answers Leading to Foolscap with Five-pointed Collar N.a
Does the collar have four points?									NO
Are the roundels in a pyramid configuration (one on top and two on bottom)?									YES
Are the peaks of the cap divided by stripes?									YES
Does the frontmost collar point meet the collar at an angle?									NO
Do the bells have stripes?									NO
Does the braid end in a circle?									YES
Do the letters “IC” appear near the roundels?									YES

To help interpret the features cited in these questions, refer to figure 14. The decision-tree path highlighted in figure 27 terminates with a designation of the subvariant as N.a. The watermark comparison in figure 26 indicates that The Frick Collection’s Jan (Johannes) Lutma the Elder has watermark N.a.b. This identification is consistent with the chainspace pattern match in figure 28.

Hinterding cites only one impression of Jan (Johannes) Lutma the Elder with this watermark (N.a.b) and one impression of the same print with the twinmark (N.a.a). The impression with the N.a.b watermark is state i. The impression with the N.a.a watermark is state ii. Both states are dated 1656.²⁴ The Frick Collection’s impression is the third in this batch.²⁵

The Frick Collection’s impression is state iii, as it contains an added inscription of François Lutma, and, therefore, was printed while the plate was no longer in Rembrandt’s possession.²⁶ State i was made by Rembrandt. This suggests that either Lutma and Rembrandt somehow bought the same paper or Rembrandt could have still been working closely with Lutma when the print was made. However, the fact that the papers for all three states are batchmates favors a continued connection between François Lutma and Rembrandt.²⁷

Landscape with Haybarn and Flock of Sheep

The Frick Collection’s impression of Rembrandt’s Landscape with Haybarn and Flock of Sheep and its beta-radiograph appear in figure 6. The watermark appears at the edge of the beta-radiograph and is just a fragment of a foolscap.

There are only two types of watermarks in Hinterding’s catalogue that have the cross atop a pyramid of three roundels: Foolscap with Five-pointed Collar and Foolscap with Seven-pointed Collar. All of the Foolscaps with Seven-pointed Collar watermarks have either a bent crosspost (i.e., the vertical component of the cross) or a “4” that incorporates the horizontal crossbar. The watermarks in figure 26 have this “4” that the fragment in figure 6 does not. The watermark fragment in figure 6 also has a straight crosspost. Therefore, the fragment in figure 6 must be from a Foolscap with a Five-pointed Collar.

With respect to a fragment lacking so much of the upper portion, the first question in the Foolscap with Five-pointed Collar decision tree in figure 16, about the number of collar points, cannot be answered. To proceed we need a modified strategy, as indicated by the flowchart in figure 17. Our approach taken here, which is a prototype for applying decision-tree-style questions to a fragment, is to begin by answering all of the questions from the decision tree in figure 16 that can be answered for the fragment of interest, which is shown in a close-up in the left half of figure 30.

All Questions in Foolscap with Five-pointed Collar Decision Tree Answerable for Fragment in Figure 30
Is there a “4” extending from the central collar point (that incorporates the horizontal crossbar)?									NO
Is there a chain line through the center of the watermark?									NO
Do the letters “IC” appear near the roundels?									NO
Do the letters “MG” appear near the “4” (just below the horizontal crossbar)?									NO
Are the roundels in a pyramid configuration (one on top and two on bottom)?									YES

Any subvariants with answers opposite to those for any of the five questions posed above can be removed from the list of possibilities. Consider, for instance, the first question. With the answer for the watermark of interest being “no,” none of the watermarks with a “4” will match the mark in question. The watermarks with a “4” include variants A, B, C, D’, E, F, G, H, I, J, L, M, N, O, and U, and twins K.b.a and K.b.b. The second question, about the presence of a chain line down the middle of the watermark, with an answer of “no” for the watermark of interest, removes variants D’ and Q’ from further consideration. As the first question already removed variant D’ from consideration, the second question just removes Q’. The presence of the letters “IC” or “MG” (from answering the third or fourth questions with “yes”) only removes, respectively, variant J and subvariant G.a from consideration. But they were already removed by the first question. Similarly, answering “no” to the roundels-in-a-pyramid question only removes variant I, which was also removed by the first question. Thus, as illustrated in figure 29, only the first two of the five questions need be asked. These two questions alone remove all possibilities that do not produce answers to all five questions that match the answers for the watermark of interest.²⁸

Subsequently, the remaining candidate subvariants of a Foolscap with Five-pointed Collar are K.a, K.c, K.e, K.f, K.h, K.i. For this reduced set of possibilities we will create a sequence of new location-appropriate questions that distinguish the fragment of interest from the remaining subvariants.

New Questions for Fragment in Figure 30 Leading to Foolscap with Five-pointed Collar K.a
Are there any kinks or curves in the crosspost?									NO
..... Subvariants remaining: K.a, K.c, K.h
Is there a crossbar?									YES
..... Subvariants remaining: K.a, K.c
Is the length of the crossbar more than half of the chainspace it is contained within									YES
..... Subvariant remaining: K.a

The full path is illustrated in figure 29. This procedure indicates a subvariant designation of K.a. The watermark comparison in figure 30 supports the identification of the fragment as K.a.a. The chainspace pattern match in figure 31 supports this designation of K.a.a.

No other impressions are cited in Hinterding’s catalogue of the same print with this watermark or its twinmark.²⁹ However, there are eighty-seven impressions of twenty-six prints with subvariant K.a and/or the associated countermark LB.a. This batch is dated to around 1650.³⁰ Interestingly, the plate date in The Frick Collection’s Landscape with Haybarn and Flock of Sheep matches this batch date.

The Goldweigher’s Field

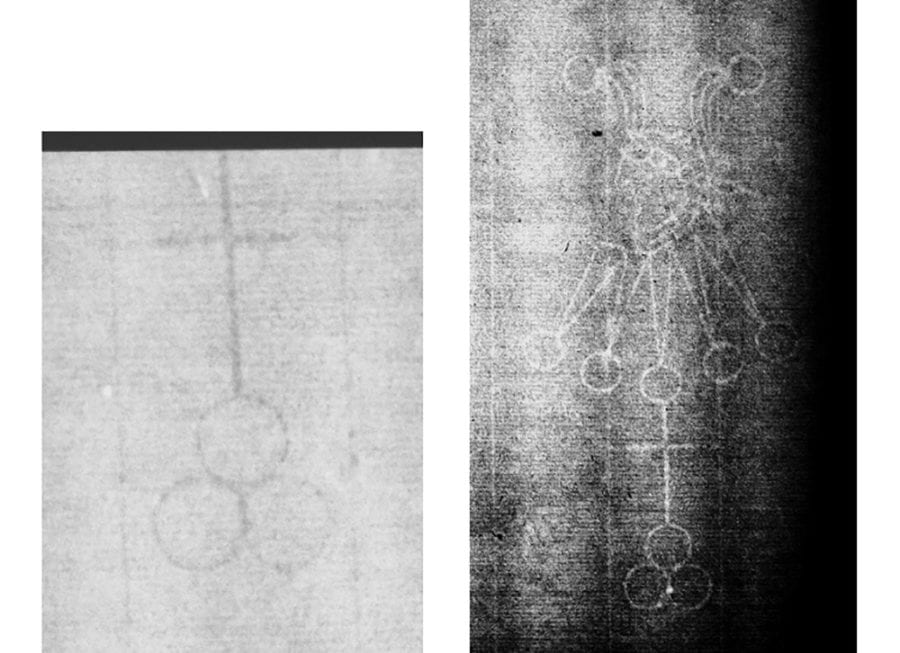
The watermark in The Frick Collection’s impression of The Goldweigher’s Field is another fragment. It appears to the left on the upper edge of the radiograph in the figure 7. Like the Foolscap with Five-pointed Collar watermark fragment in Landscape with Haybarn and Flock of Sheep, the Paschal Lamb fragment in The Goldweigher’s Field is of the bottom portion of the watermark, as is apparent in figure 7. The difference with The Frick Collection’s Landscape with Haybarn and Flock of Sheep is that the fragment in The Goldweigher’s Field has a larger portion of the full Paschal Lamb watermark, and the first few questions in the Paschal Lamb decision tree in figure 32 can therefore be answered. Labels for some Paschal Lamb features are illustrated in figure 33. A close-up of the watermark appears on the left in figure 35.

A string of three questions at the top of the Paschal Lamb decision tree in figure 32 can be answered for the fragment in figure 35.

Initial Sequence of Questions in the Paschal Lamb Decision Tree Answerable for Fragment in Figure 35
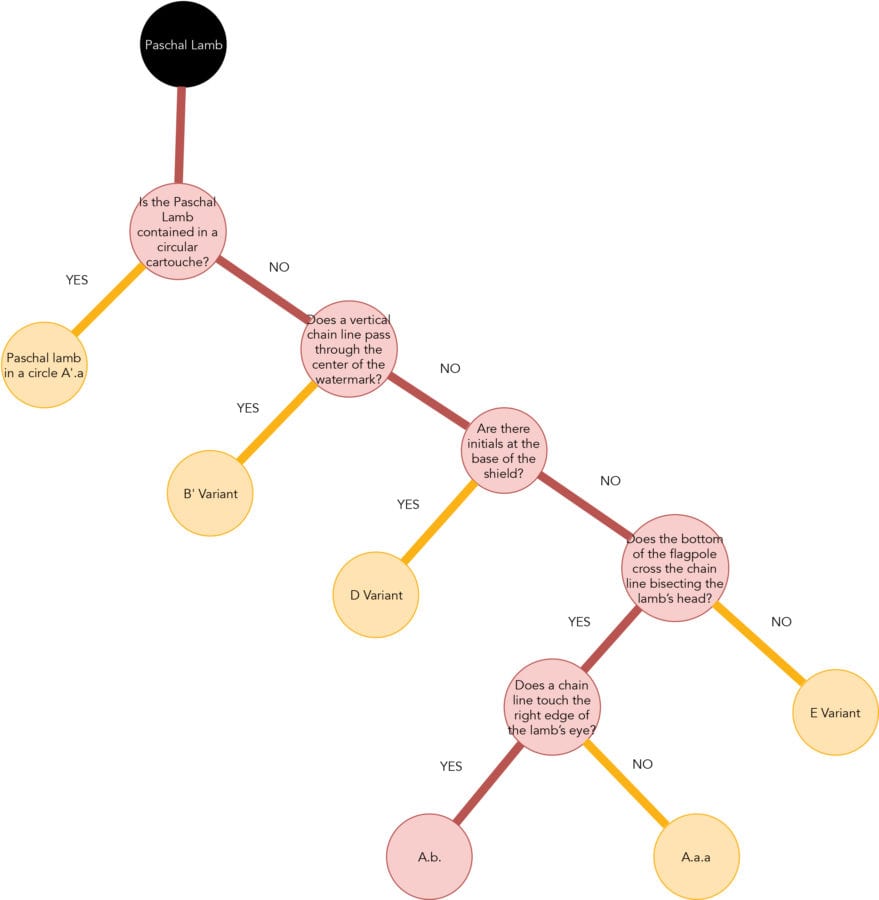
Is the Paschal Lamb contained in a circular cartouche?									NO
Does a vertical chain line pass through the center of the watermark?									NO
Are there initials at the base of the shield?									NO

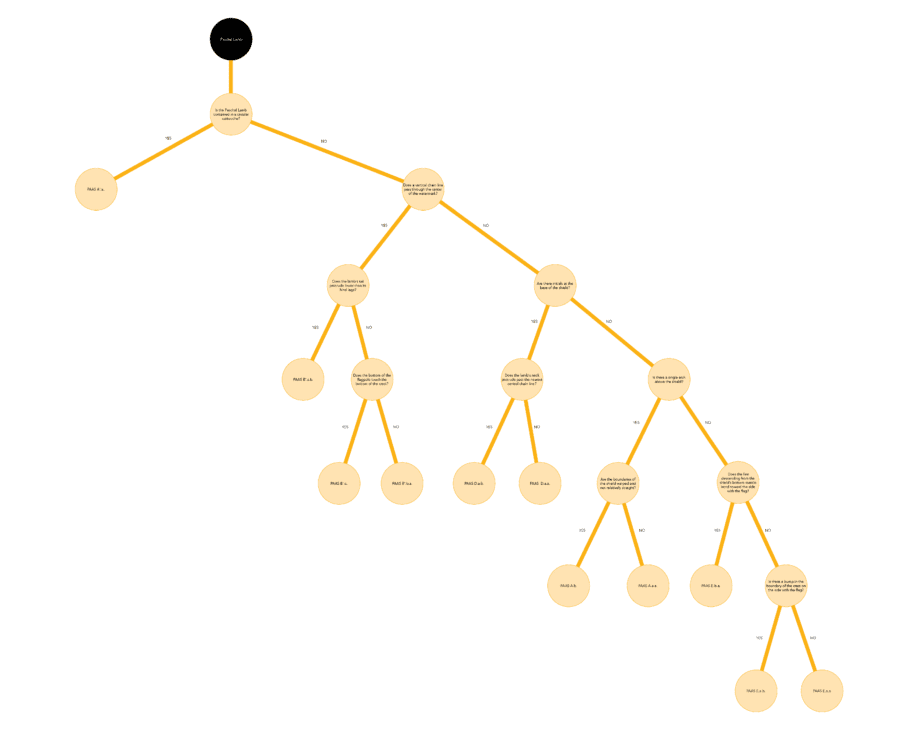
At this point in the tree the only remaining destinations are A.a.a, A.b, E.a.a, E.a.b, E.b.a. Our strategy is to create a continuing sequence of new location-appropriate questions (with watermark orientation set by figure 33, thereby allowing the use of “bottom” and “right” in the questions selected) that distinguish the fragment of interest from as many of these remaining subvariants as possible.

New Questions for Fragment in Figure 35 Leading to Paschal Lamb A.b
Does the bottom of the flagpole cross the chain line bisecting the lamb’s head?									YES
..... Subvariants/twins remaining: A.a.a, A.b
Does a chain line touch the right edge of the lamb’s eye?									YES
..... Subvariant remaining: A.b

The full path for this fragment is illustrated in figure 34. This procedure indicates a subvariant designation of A.b. Comparing the watermark of interest to the Paschal Lamb A.b in figure 35 supports the answer from the decision tree. The chainspace pattern matching in figure 36 also supports a designation of A.b.

All Paschal Lamb A variants are probably various twinmarks in stages of deformation and therefore all batchmates.³¹ The Goldweigher’s Field appears five times on Paschal Lamb A.a.a, two times on A.a.b, three times on A.a, four times on A.b, and once on A.c.³² Thus, The Frick Collection’s impression of The Goldweigher’s Field is the fifth impression of the same print with the Paschal lamb A.b watermark. Hinterding cites sixty-two impressions of fourteen prints using Paschal Lamb A.a, A.b, or A.c and/or its countermark RC.a and dates the batch to 1651.³³

Clement de Jonghe

The Frick Collection’s Clement de Johnge has an RC countermark, as illustrated in figure 8. A close-up of the countermark appears on the top in figure 37. Hinterding cites only one variant (RC) for the RC countermark, which has only one subvariant (RC.a), and three twinmarks (RC.a.a, RC.a.b, and RC.a.c).³⁴ Thus, a decision-tree branch is unnecessary in claiming that the subvariant is RC.a. The watermark comparison in figure 37 and the chainspace pattern comparison in figure 38 support a designation of RC.a.a.

Hinterding lists seven impressions of Clement de Jonghe with countermark variant RC.a, not including The Frick Collection’s impression, and states that it is the countermark to Paschal Lamb variant A.³⁵ As noted in the preceding discussion of The Goldweigher’s Field, all subvariants of Paschal Lamb A are considered to be batchmates and, thus, have the same date of creation: 1651. Because The Goldweighers Field has a Paschal Lamb A watermark and Clement de Jonghe has an RC.a.a countermark, these impressions are batchmates.

St. Francis Praying Beneath a Tree

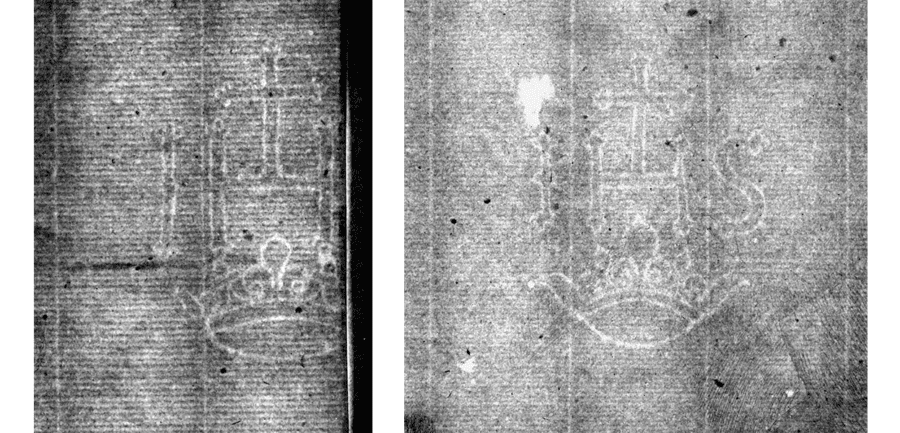
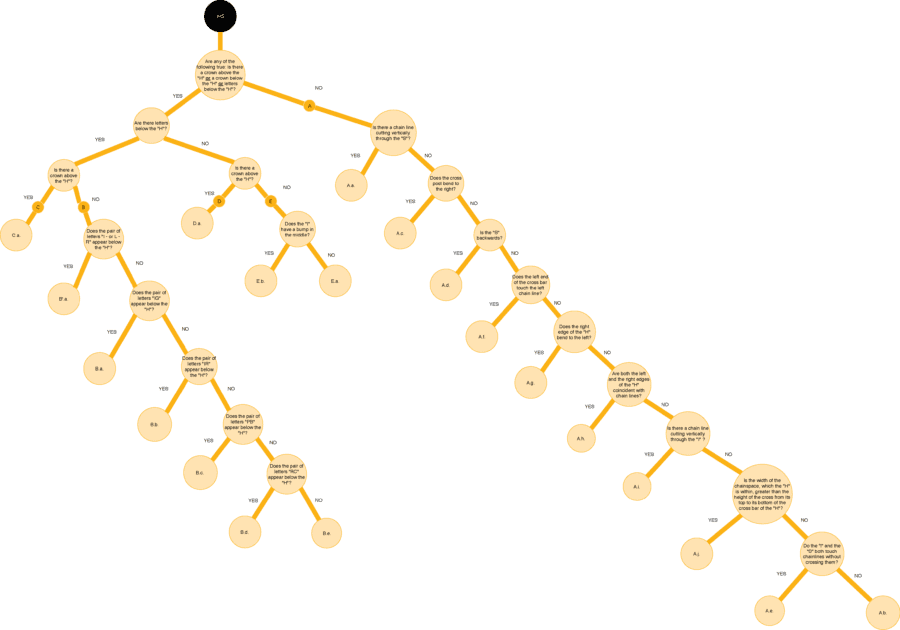
The Frick Collection’s impression of Rembrandt’s St. Francis Praying Beneath a Tree and its beta-radiograph appear in figure 9 with a close-up of the watermark on the left in figure 49. The IHS countermark appears in the center of the beta-radiograph. IHS is always a countermark and has five variants and twenty-two subvariants.³⁶ The IHS countermark will be used here as an illustration of decision-tree construction using a decision table like the one in Table 1.³⁷

IHS Decision Table as Construction Aid for Decision Tree

In developing a decision tree, we follow a layered approach suited to the hierarchy of Hinterding’s taxonomy.

1.   Using a group of images containing one representative sample from each variant, develop questions about scale-invariant features that first separate the entire set of IHS watermarks into the variant categories.

2.   Confirm that these questions work for all members (subvariants and twins) of each variant by sorting them into their correct variant.

3.   For each variant, develop questions that next separate the watermarks by subvariant.

4.   Confirm that these questions work for all members (twins) of each subvariant by sorting them into their correct subvariant. (There is no need to distinguish twins if the watermark identification is to be used for dating, as twins will occur together in the same batch of paper and will be used in the same time period.)

To help select features used to transition from type to variant, one sample of each IHS variant is included in figure 39. Given that Hinterding’s taxonomy is based on human decisions, the features distinguishing the variants should be readily observable, such as the following list of distinctions:

•  IHS with cross mounted on cross bar of H; no crown above or below H and no letters below H
•  letters below H and no crown above or below H
•  crown above and letters below H
•  crown above H and no letters below H
•  crown below H and no letters

Hinterding provides a list of features possessed by each IHS variant:³⁸

A.    The initials IHS, double-wired, a Latin cross above the H
B.     Initials below the IHS
C.     A crown above the Latin cross, initials below
D.    As above (with the crown), but with no initials below
E.     A crown below the initials

In this case these features correspond closely to our observations.³⁹

The observed distinctions for variant separation can be captured by the following basic questions:

Q01: Are there letters below the H?
Q02: Is there a crown above the H?
Q03: Is there a crown below the H?

Table 2 lists binary answers for these three questions with “yes”=1 and “no”=0. Each answer listed for a particular variant is the answer to that question for every subvariant as well. The resulting binary code for each variant in the rows of Table 2 is unique.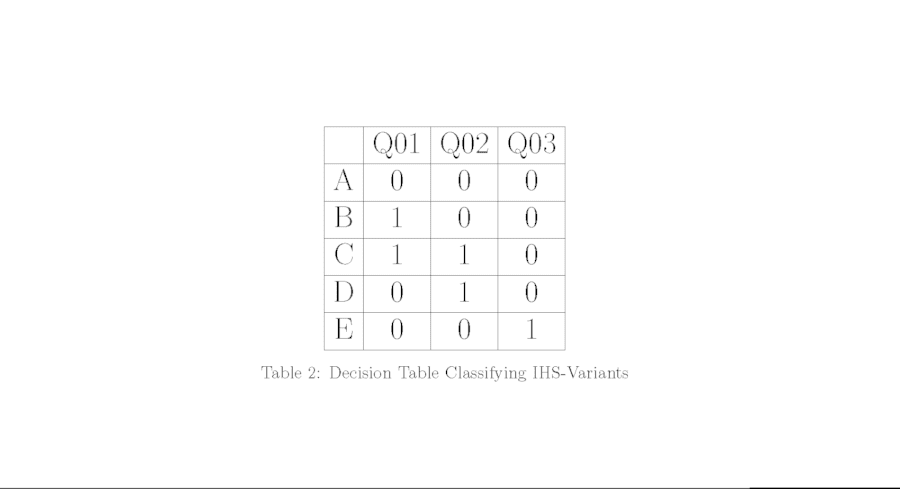

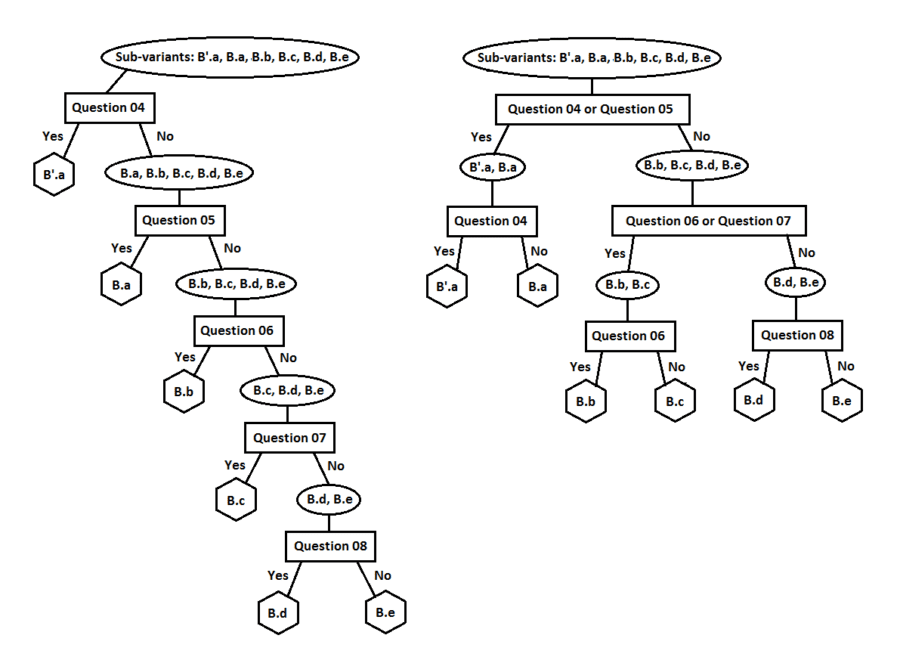
Various orderings of the three questions distinguishing the variants of IHS can offer satisfactory decision-tree options. Two possibilities are illustrated in figure 40. Given that the variant A has more than half of the subvariants, the decision tree in the right diagram in figure 40 might provide a way to reduce the average number of questions needed to reach an end point in the decision tree.

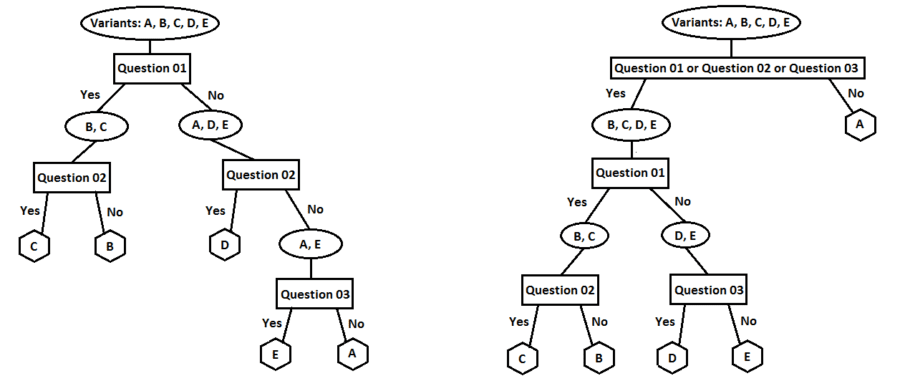
The decision tree on the right in figure 40 includes a combination of all three questions in a logical “OR” configuration as its first inquiry. In this case, if the answer to any of the three questions is “yes,” then the answer to their combination is “yes.” Conversely, if the answer to all of the three questions is “no,” then the answer to “Question 01 OR Question 02 OR Question 03” is “no.” The use of a logical AND function is also possible, though not utilized in figure 40. For example, only if the answer to both Question A and Question B is “yes” will the answer to “Question A AND Question B” be “yes.”

Because variants C and D each have only one subvariant, no further questions are needed to identify the subvariant once either C or D has been identified as the variant. Variant E has two subvariants, so one question should suffice to distinguish the two subvariants illustrated in figure 41. One distinguishing feature is captured by the question: “Does the ‘I’ have a bump in the middle?” Figure 41 would be made available to the user of the decision tree, with the location of the “bump” (if present) highlighted on each of the two subvariants as an aid in distinguishing the “yes” image from the “no” image. (Such Yes/No samples were presented in figures 20–24 to help identify Foolscap with Five-pointed Collar variant A.) The wording of this question provides an example of how a more precise labeling than the generic use of “bump” might increase confidence in the user’s answer.⁴⁰ Answering “yes” identifies E.b and “no” indicates E.a.

All six subvariants of variant B have letters below the “H” in “IHS,” as illustrated with a sample from each subvariant in figure 42. The pairs of letters are a distinguishing feature that allows the same question to be asked repeatedly about a different pair of letters.

Questions 04-09: Does the pair of letters XX appear below the H?
Q04	YES for reversed letters IR (or LR?), B.a						NO for all others
Q05	YES for IG, B.a						NO for all others
Q06	YES for IR, B.b						NO for all others
Q07	YES for PB, B.c						NO for all others
Q08	YES for RC, B.d						NO for all others
Q09	YES for ET, B.e						NO for all others

This creates the decision table in Table 3.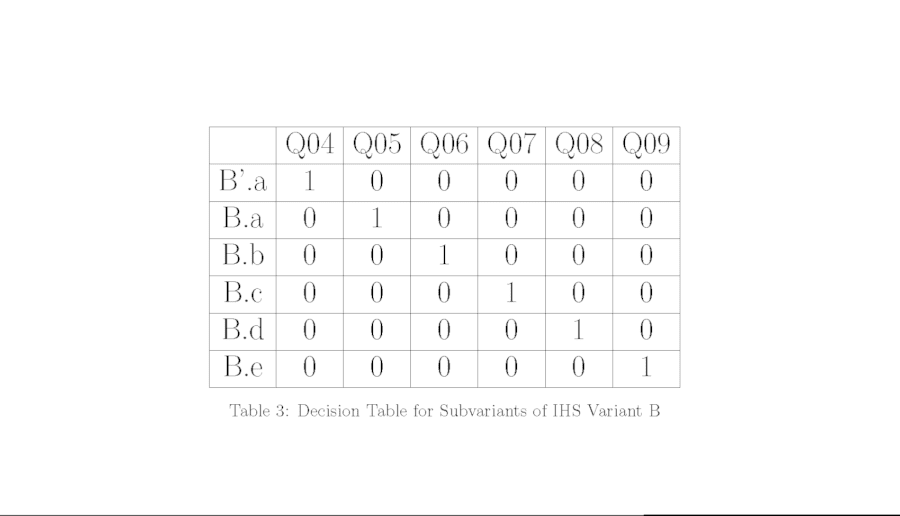

As each column in Table 3 has only one nonzero entry, asking any five questions in any order will produce a decision tree classifying the subvariants of variant B, as in the left diagram in figure 43. Each of these five questions has only one choice among the five subvariants for which the answer is “yes.” We will label such questions, for which only one subvariant generates the answer “yes” and all others have the opposite answer “no,” as a “singular-yes” question. Other “singular-yes” questions are possible, such as questions about certain individual letters or about a chain line down the center of the countermark, which separates out B’.a.⁴¹

Samples of the subvariants of IHS variant A are illustrated in figures 44–45. We will start with as many “singular-yes” questions as we can readily derive from close looking. It is worth recalling that all questions need to be answerable with high confidence for all subvariants. The feature labels in figure 46, which exemplifies the chosen orientation, are used in the following questions.

Questions 10-17: Singular-Yes Questions
Q10: Is there a chain line cutting vertically through the “S”?			YES, A.a	NO, all others
Q11: Does crosspost bend to right?			YES, A.c	NO, all others
Q12: Is the “S” backwards?			YES, A.d	NO, all others
Q13: Does the left end of the crossbar touch the left chain line?			YES, A.f	NO, all others
Q14: Does the right edge of the “H” bend to left?			YES, A.g	NO, all others
Q15: Are both the left and right edges of “H” coincident with chain lines?			YES, A.h	NO, all others
Q16: Is there a chain line cutting vertically through the I?			YES, A.i	NO, all others
Q17: Is the width of the chainspace, which the “H” is within, greater than the height of the cross from its top to the bottom of the cross bar in H? [Hint: Implement with marks made on the straight edge of a piece of paper placed adjacent to the watermark image.]			YES, A.j	NO, all others

With eight singular-yes questions and nine subvariants to identify, we now form the decision table in Table 4 in order to see what remains to be done if we are to differentiate the various subvariants from one another. Because A.b and A.e have the same (eight zeros) code in Table 4, we just need to add a question that has different answers for A.b and A.e in order to produce a decision table with each subvariant having a different binary code.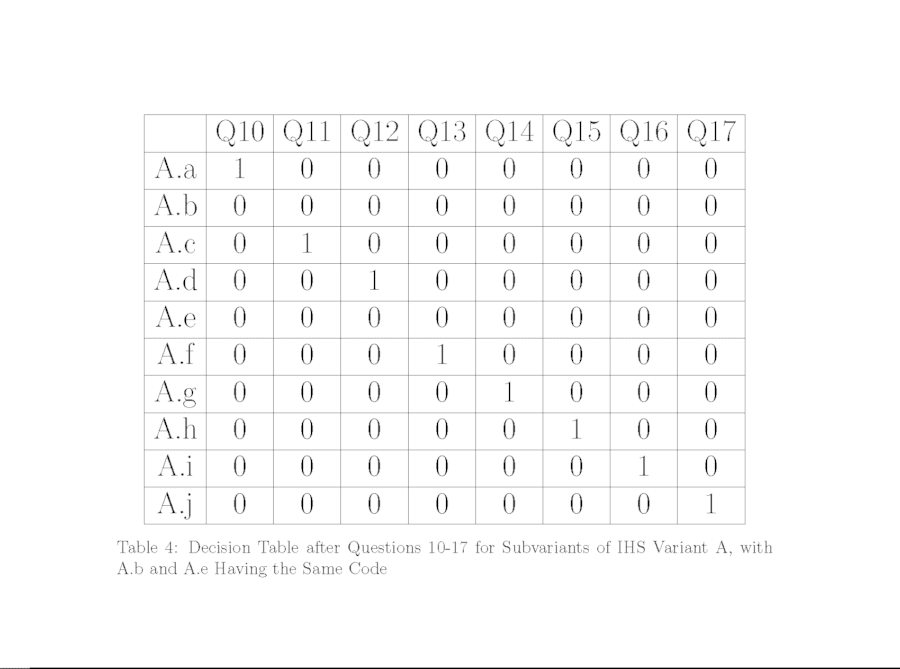

For example, consider the following question.

Question 18
Q18: Do the “I” and the “S” both touch chain lines without crossing them?		YES, A.c, A.e, A.f, A.g;	NO, all others

Adding this eighteenth question to the partial decision table in Table 4 results in the decision table in Table 5, where each subvariant has a unique binary code. The decision tree for IHS, incorporating the questions in Table 5, asked in their numerical order, appears in figure 47.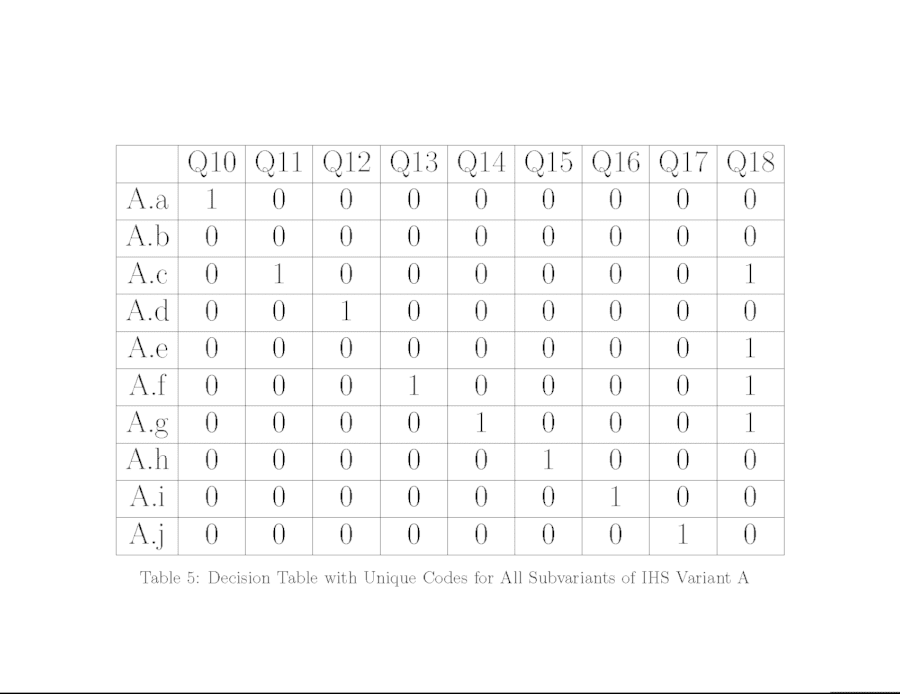

As a final note, two important decision-tree construction guidelines for the procedure embodied by the preceding example, of selecting distinguishing features for a layered decision tree, are:

Questions for type to variant layer must be confidently answerable, with the same answer (yes or no) for all subvariants of that variant.

Questions for variant to subvariant layer must be confidently answerable, with the same answer (yes or no) for all twins and nearly similar watermarks of that subvariant.

Returning to Analysis of St. Francis Praying Beneath a Tree

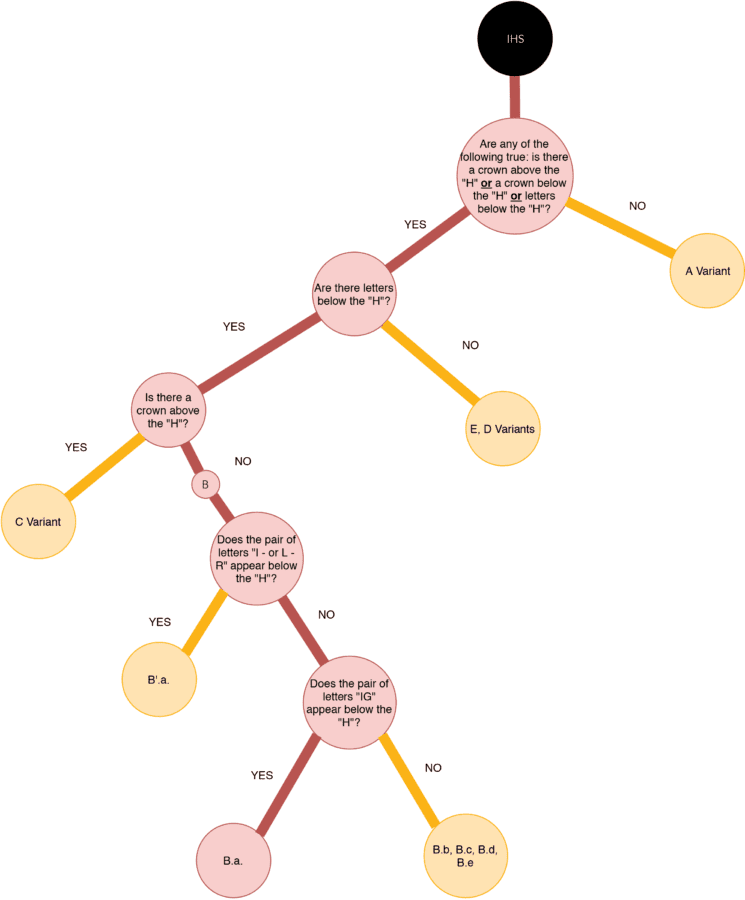
Answering five questions in the IHS decision tree in figure 47 identifies the countermark in the left half of figure 49.

Questions and Answers Leading to IHS B.a
Is there a crown above the “H,” a crown below the “H,” or letters below the “H”?									YES
Are there letters below the “H”?									YES
Is there a crown above the “H”?									NO
Does the pair of letters “IR” (or “LR”) appear below the “H”?									NO
Does the pair of letters “IG” appear below the “H”?									YES

The path to the subvariant designation of B.a is illustrated in figure 48. The countermark comparison in figure 49 and chainspace pattern match in figure 50 are consistent with a designation of B.a.a.

Not counting The Frick Collection’s impression, Hinterding cites two prints and four impressions with the countermark IHS B.a.a and its twin B.a.b.⁴² The Frick Collection’s St. Francis Praying Beneath a Tree is the second impression of the same print with this countermark.

Landscape with Three Gabled Cottages

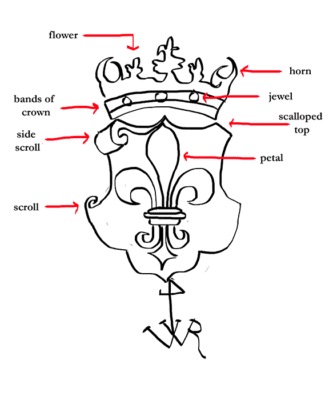
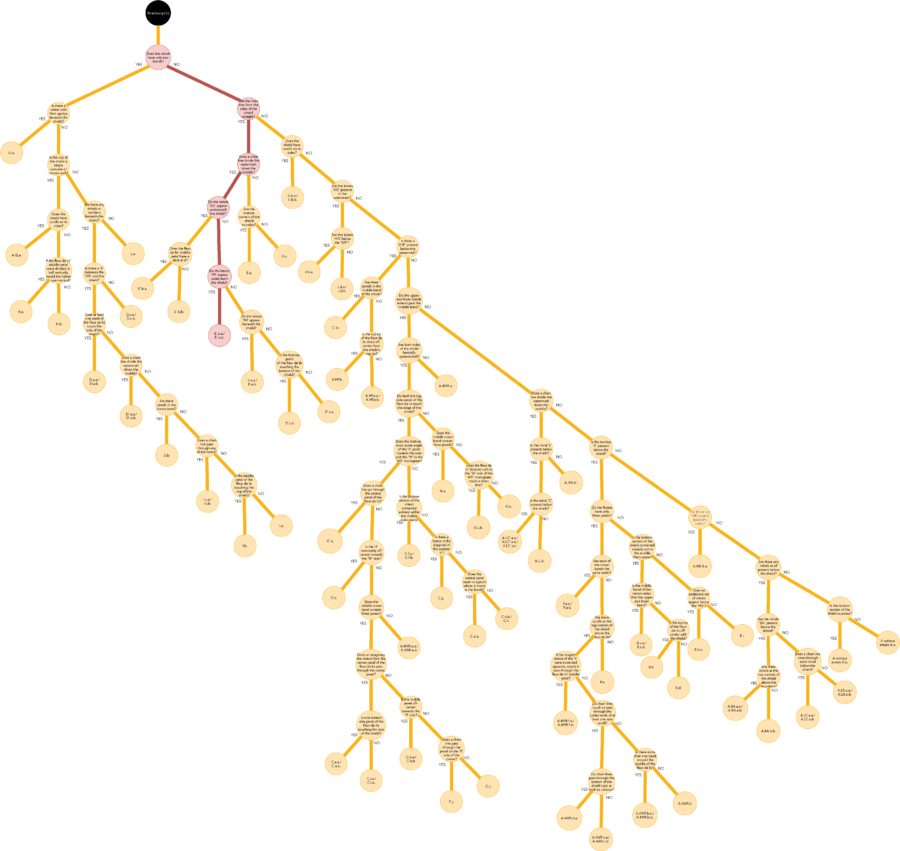
Figure 10 reveals that The Frick Collection’s Landscape with Three Gabled Cottages has a Strasbourg Lily watermark (fig. 53). Strasbourg Lily is a frequently occurring watermark in Rembrandt’s etchings, with sixteen variants.⁴³ A sketch of the Strasbourg Lily watermark, with feature labels, appears in figure 51. The full Strasbourg Lily decision tree appears in figure 52.

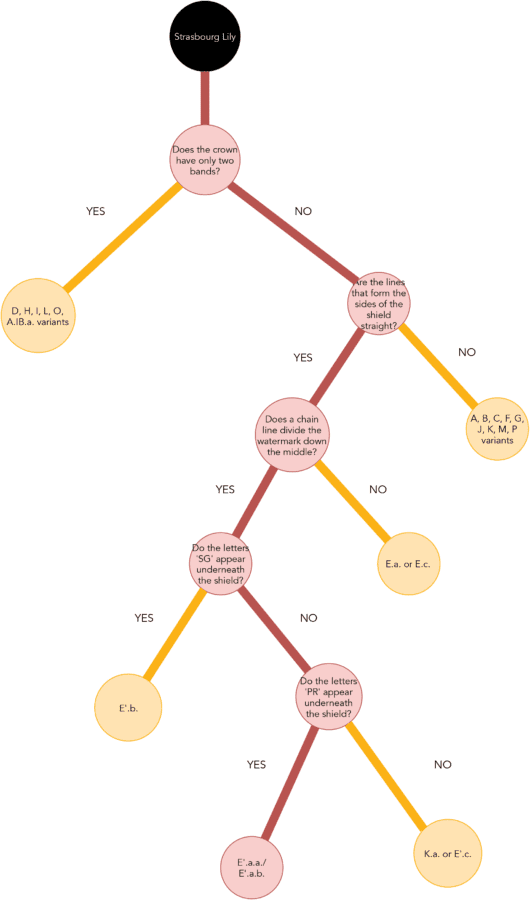
Answering five questions in the Strasbourg Lily decision tree in figure 52 identifies the watermark under investigation in figure 53.

Questions and Answers Leading to Strasbourg Lily E'.a
Does the crown only have two bands?									NO
Are the lines that form the sides of the shield straight?									YES
Does a chain line divide the watermark down the middle?									YES
Do the letters “SG” appear underneath the shield?									NO
Do the letters “PR” appear underneath the shield?									YES

The decision-tree branch in figure 54 indicates a variant designation of E’.a. Answering the question “Does the ‘P’ side of the shield overlap with the chain line?” in the affirmative identifies the label, including the subvariant indicator, as E’.a.a. The watermark comparison in figure 53 and the chainspace pattern comparison in figure 55 support this designation. The apostrophe on the variant designation E’ indicates that the watermark has a chain line down its center.

Hinterding cites nineteen prints with Strasbourg Lily watermark subvariant E’.a.a, including one impression of Landscape with Three Gabled Cottages, and twenty prints with its twin E’.a.b, including three impressions of Landscape with Three Gabled Cottages.⁴⁴ Thus, The Frick Collection’s Landscape with Three Gabled Cottages is the second impression of the same print with this watermark. As Strasburg Lily E’.a.a is known to have a WK’.a countermark, Hinterding lists 115 impressions of twenty-seven prints in the batch dated circa 1652.⁴⁵

Detailing Discoveries among Seven Prints in The Frick Collection

Having surveyed our decision-tree creation and exploitation process for seven prints in The Frick Collection, we can now return to our observations earlier in this article and rephrase them in greater detail.

Landscape with Haybarn and Flock of Sheep has a Foolscap with Five-pointed Collar K.a.a watermark. This leads to a date of circa 1650 using Hinterding’s chronology. No other impressions of this print with this watermark or its twinmark were reported by Hinterding.

Landscape with Three Gabled Cottages has a Strasbourg Lily E’.a.a watermark, which prompts a date of circa 1652 in Hinterding’s chronology.⁴⁶ Hinterding reports that impressions from nineteen different plates appear on paper with this watermark.

The Goldweigher’s Field and Clement de Jonghe are batchmates. Clement de Jonghe has the subvariant class RC.a mark, which is the countermark associated with watermark Paschal Lamb A variants. The Goldweigher’s Field has the watermark Paschal Lamb A.b.

Jan (Johannes) Lutma the Elder is state iii and has the watermark N.a.b, as do states i and ii. State i was actually printed by Rembrandt, but the inscription on state iii suggests that possession of the plate had shifted to the sitter’s family. The use of the same paper for all three states raises various possible scenarios leading to this fact.

Furthermore, we were able to identify all of the marks in the seven prints examined—watermarks in five prints as well as countermarks in the other two. The following list notes the watermark identified by WIRE and also, when possible, the date assigned by Hinterding to the watermark or countermark.

Landscape with Three Trees has the watermark Foolscap with Five-pointed Collar A.a.a, which is dated 1643.

Jan (Johannes) Lutma the Elder has the watermark Foolscap with Five-pointed Collar N.a.b, which is dated 1656.

Landscape with Haybarn and Flock of Sheep has the watermark Foolscap with Five-pointed Collar K.a.a, which is dated 1650.

The Goldweigher’s Field has the watermark Paschal Lamb A.b, which is dated 1651.

Clement de Jonghe has the countermark RC.a.a, which is dated 1651.

St. Francis Praying Beneath a Tree has the countermark IHS B.a.a, which is not dated in Hinterding’s chronology.

Landscape with Three Gabled Cottages has the watermark Strasbourg Lily E’.a.a, which is dated circa 1652.

WIRE Discoveries of New Watermarks

During the decision-tree development the WIRE Project has unearthed a variety of “new” watermarks. The first category of discoveries includes new impressions of prints from the same plate/state with a watermark previously associated with the print. This increases the counts of usage of paper with that particular watermark for that print. The Frick Collection’s Landscape with Three Trees, Jan (Johannes) Lutma the Elder, St. Francis Praying Beneath a Tree, The Goldweighers Field, Clement de Jonghe, and Landscape with Three Gabled Cottages are all examples of this category.

The second category includes prints with watermarks not previously associated with that print but found in other prints, thereby adding to the known works with that particular watermark, with its own particular date. The Frick Collection’s Landscape with Haybarn and Flock of Sheep is an example of this second category.

A third category includes any print bearing a previously unknown type, variant, or subvariant in Rembrandt’s papers not documented by Hinterding. This category would indicate the existence of a previously unknown batch of paper. Though no discoveries of this third category occur in the prints studied from The Frick Collection, the WIRE Project has made such discoveries elsewhere. For example, in the collection of the Herbert F. Johnson Museum at Cornell University, the WIRE Project has discovered a new subvariant of the Basel Crosier watermark with proposed label E’.b. This has been found in Rembrandt’s Self-Portrait (?) with Plumed Cap and Lowered Sabre.⁴⁷

Going Forward

The decision tree being developed by the WIRE project confirms that both the features chosen and the questions asked about them are sufficient to distinguish all of the subvariants among the watermarks in etchings by Rembrandt that Hinterding examined. The decision tree also offers another advantage with its use in establishing that a particular watermark is not included in Hinterding’s published taxonomy. This is possible because Hinterding did not examine every extant Rembrandt print. Once the termination point of a decision-tree branch has been reached, assuming all questions have been answered correctly, the answers to the string of yes/no questions traversed is shared by no watermark in the full library other than the subvariant (or twin) indicated at the termination point. If the user finds that the sample image at the termination point does not match both the watermark being identified and its chainspace pattern, then the user can be assured that the watermark under consideration is new to scholars of Rembrandt’s prints.⁴⁸

This decision-tree process of identifying watermarks raises a variety of issues for further investigation. These include:

Automation of Watermark Identification: A decision tree for a particular variant contains a number of yes/no questions, the answers to which are verifiable by a human observer. Can image processing be used to answer questions that are simple for a human to answer but appear quite complicated for a computer to answer with similar confidence? Such automation should retain the use of an identifying yes/no visible feature-question string and Hinterding’s classification taxonomy.

Data Collection: The WIRE Project team has considered using the decision tree to identify the watermark in an owner’s Rembrandt in exchange for permission to post the image of the watermark in the planned online version of the decision-tree identification tool and dataset. One research/development goal to boost this effort would be the fabrication of a modestly priced, portable imaging device that captures watermarks, chain lines, and laid lines without radiography.⁴⁹ The assembled dataset should include as many examples as possible of each specific watermark.⁵⁰

A Dynamic Decision Tree: Incorporating new watermarks discovered in collections beyond those catalogued by Hinterding raises the issue of standardizing a procedure for augmentation of the decision tree.⁵¹ This need for such decision-tree growth faithful to the architecture of Hinterding’s taxonomy while retaining his labels is an unusual twist on basic decision-tree theory.

Extension of Batchmate Identification to Laid Papers without Watermarks: Since approximately two-thirds of Rembrandt’s impressions do not have watermarks or fragments, it would be hugely advantageous to develop some technique of connecting laid papers that are batchmates but have no watermarks to papers with a specific watermark. One path could be to assemble an image revealing chain lines, watermark, and countermark (if present) of a full broadsheet, perhaps from constituent folio images, and attempt to match paper without watermarks to portions of the full broadsheet lacking a watermark. The main impediment here is that museums are not inclined to image paper supports without watermarks.

New Tools Aiding Visual Moldmate/Batchmate Verification: One restriction in human-selected features is a justifiable lack of confidence in visually assessing the relative distances within one figure between two pairs of endpoints. Such doubt is a measure of the human susceptibility to optical illusions. This could be overcome by the ability to mouse click on the endpoints and have the computer evaluate the ratio of the lengths (e.g., in pixels) of the two line segments. Using a ratio bypasses the need for precise physical measurement capability, which would require some care in imaging and/or digitization.

Extension to Other Maker’s Marks: Decision trees should be useful in a variety of cultural heritage tasks, such as the identification of maker’s marks. One potential application that shows promise is the further identification of panel maker marks and guild brands.⁵²

Expanding the Rembrandt Watermark Universe: Assuming Rembrandt would sometimes use the same paper for prints and drawings, collecting a dataset of watermarks in Rembrandt’s drawings seems appropriate and could possibly provide valuable insights into the artist’s working method. The expansion should also consider prints and drawings by pupils and collaborators, who may have shared materials with Rembrandt and each other. Watermarks have been found in two drawings by Rembrandt’s pupil, Ferdinand Bol, that appear in prints by Rembrandt.⁵³ It should be noted that expansion to include other Dutch artists active in Rembrandt’s time in Amsterdam is also appealing. One concern is that such a proliferation may include a vastly increased variety of highly similar, but distinct, watermarks, making unaided visual classification impractical. Simple-to-use, computer-based tools designed for the specific tasks of watermark feature evaluation and comparison will help address this concern.

Appendix: Provenance,⁵⁴ States,⁵⁵ and Links to Online Catalogue Entries

The links provided to the online catalogue of The Frick Collection include the Bartsch number, the date assigned by The Frick Collection, the technique and medium, and the print’s measurements.

Landscape with Three Trees, The Frick Collection, 1915.3.28
Alfred Strolin. Knoedler. Frick, 1915
only state
https://collections.frick.org/objects/646/landscape-with-three-trees

The Goldweigher’s Field, The Frick Collection, 1915.3.31
Colnaghi. Knoedler. Frick, 1915
only state
https://collections.frick.org/objects/647/the-goldweighers-field

Landscape with Haybarn and Flock of Sheep, The Frick Collection, 1916.3.29
Colnaghi. Knoedler. Frick, 1916
state ii of ii (2/2)
https://collections.frick.org/objects/640/landscape-with-haybarn-and-flock-of-sheep

Landscape with Three Gabled Cottages, The Frick Collection, 1916.3.30
Knoedler. Frick, 1916
state iii of iii (3/3)
https://collections.frick.org/objects/641/landscape-with-three-gabled-cottages

St. Francis Praying Beneath a Tree, The Frick Collection, 1916.3.35
H. Danby Seymour and Alfred Seymour (Lugt 176). Knoedler. Frick, 1916
state ii of ii (2/2)
https://collections.frick.org/objects/642/st-francis-praying-beneath-a-tree

Clement de Jonghe, The Frick Collection, 1916.3.36
Colnaghi. Knoedler. Frick, 1916
state i of x (1/10)
https://collections.frick.org/objects/643/clement-de-jonghe

Jan (Johannes) Lutma the Elder, The Frick Collection, 1916.3.37
Pierre Mariette (Lugt 1788-90, dated 1670). Knoedler. Frick 1916.
state iii of v (3/5)
https://collections.frick.org/objects/644/jan-johannes-lutma-the-elder-ca-15841669

Acknowledgements

I wish to express my gratitude to Robert van Langh (Head of the Department of Conservation and Restoration, Rijksmuseum, and Chair of the Netherlands Institute for Conservation, Art and Science [NICAS]), as well as the Rijksmuseum, for my appointment as a Scientific Researcher of the Rijksmuseum since 2013. This appointment facilitated my interaction, which began in 2013, with Erik Hinterding (Curator of Prints, Rijksmuseum).

The WIRE Project emerged from examination of an attempt to use the chain line pattern as an identifier of the laid-paper supports of Rembrandt’s prints, a task I began in 2012 with Margaret Holben Ellis (Eugene Thaw Professor of Paper Conservation, New York University). The results of this early work were initially reported at the conference New Directions in the Study of Rembrandt and His Circle held at the Bader International Study Centre, Herstmonceux Castle, East Sussex, UK, July 18–21, 2013, and subsequently published in revised form.⁵⁶ At this conference, I met Nadine M. Orenstein (Drue Heinz Curator in Charge of Prints and Drawings at the Metropolitan Museum of Art), who offered to assist by providing images of watermarks in Rembrandt’s prints in the Met’s collection. These watermark images were added to the beta-radiographs of Rembrandt prints in the collection of The Morgan Library & Museum provided by Reba Fishman Snyder (Paper Conservator, The Morgan Library & Museum) to create our starter set for the development of computer-based algorithms for chain line pattern marking and matching. In 2014, the dataset was greatly enlarged by the access that was granted by the Dutch University of Art History (Florence, Italy) to their set of hundreds of radiographs of Rembrandt’s prints containing watermarks, a set collected by Erik Hinterding.⁵⁷ In 2015, the need to identify the watermarks in the accumulated dataset in order to check the accuracy of moldmate matching (by earlier chain line pattern analysis) resulted in the creation of the WIRE project, which I codirected from the start with Andrew C. Weislogel (Seymour R. Askin, Jr. ’47 Curator of Earlier European and American Art, Herbert F. Johnson Museum of Art, Cornell University). The WIRE Project has been fortunate to have Erik Hinterding, Margaret Holben Ellis, and Nadine M. Orenstein as advisors since its founding. In 2019, Sound & Vision Publishers BV gave the WIRE Project at Cornell permission to use their images from Hinterding’s book in research and publication. These images will also be appearing in the online version of the WIRE decision tree.

The WIRE Project was conceived as a student-powered project from its inception. I am indebted to the Cornell University students who have participated (so far) in the WIRE Project: Margaret Canfield, Isabella Dobson, Katrina Ferreira, Virginia Girard, Sara Gorske, Riley Henderson, Amanda House, Orrin Kigner, Dong Ki Kim, So Jeong Lim, Hao Lu, Anjum Malik, Elizabeth Martinson, Katarina Martucci, Alison McCann, Kira Nicolai, Margaret Orbon, Oscar Rieveling, Phoebe Ross, Jason Setter, Samantha Siegler, Nina Simpkins, Louisa Smieska, Daniel Terry, and Xuelei Xi. Teaching and guiding these students would not have been possible without my colleagues Andy Weislogel and Brittany Rubin, who are members of the curatorial staff at the Johnson Museum at Cornell.

Louisa Wood Ruby (Head of Research, Frick Art Reference Library) and Ellen Prokop (Associate Head of Research, Frick Art Reference Library) at The Frick Collection provided access to images of The Frick Collection’s Rembrandt prints and invited me to speak on the WIRE Project in December 2018 in The Frick Collection’s Digital Art History Lab Lecture series.⁵⁸ (Subsequently, in the first week of 2019, I was offered—and accepted—an appointment as Senior Research Advisor to the Frick Art Reference Library, New York, NY.) Chris Stolwijk (Director, RKD  Netherlands Institute for Art History) selected me as the 2018 RKD Visiting Fellow in Computational Art History, which resulted in my teaching a short course at the RKD, in October 2018, on identifying watermarks in Rembrandt’s etchings. Those lectures, both at The Frick Collection and at the RKD, are the basis for this paper.

I thank the editorial staff of the Journal of Historians of Netherlandish Art, in particular Alison Kettering, Bret Rothstein, Jessica Skwire Routhier, and Heidi Eyestone, for their efforts in conquering the challenges of this article with its technical core and reliance on a large collection of figures and lists.

The WIRE Project at Cornell has been supported by a National Endowment for the Humanities Digital Humanities Advancement Grant (HAA-256123-17, “Building a Decision Tree for Watermark Identification in Rembrandt’s Etchings—The WIRE Project,” October 2017–March 2020) and a National Science Foundation Early-concept Grants for Exploratory Research (EAGER) Grant (CCF-1822007, “Automated Watermark and Moldmate Identification,” March 2018–February 2020).