Two pairs of paintings by Johannes Vermeer are designated as pendants by Walter Liedtke in his catalog of Vermeer’s paintings. The canvases of one of these pairs have previously been shown to be from the same bolt, which is frequently an attribute of a pendant pair in seventeenth-century Dutch paintings. This paper provides evidence, in the form of a new weave match, that the second pendant pair identified by Walter Liedtke also exhibits this bolt-matestatus.
Introduction
A pendant is one of two paintings conceived as a pair. Paired pendants are typically of similar size, often with similar frames, and were perhaps intended to be hung together on the two sides of a door or fireplace. Pendants were often portraits of married couples (such as the Portrait of a Gentleman and the Portrait of a Lady Holding a Flower by Ferdinand Bol) though any two similar people or subjects might be used. For example, Willem van de Velde’s pendants The Cannon Shot and The Gust depict two ships sailing in different seas under different skies. Furthermore, seventeenth-century Dutch pendant pairs are often on canvas from the same bolt.1
In his catalog of the paintings of Johannes Vermeer, Walter Liedtke identified two pairs of paintings that may have been intended as pendant pairs,2 the Young Woman Standing at a Virginal paired with the Young Woman Seated at a Virginal, and The Geographer paired with The Astronomer. Both pairs are similarly sized, have similar subjects (two women and two scholars), and similar backgrounds.
Further physical evidence that the paintings of the two young women were intended to be a pendant pair is provided by a detailed analysis of the canvas. The average thread counts are similar, and the pattern of stripes in the thread-density weave maps match strikingly.3 This is consistent with the two canvases having originally been on the same bolt, thus suggesting a physical proximity that may mirror the intended pairing of the two works.
This paper continues the canvas examination by investigating the thread-density weave maps for The Astronomer and The Geographer. Again, the average thread counts and the patterns of stripes in the weave maps of the densities of the vertical threads are remarkably similar, establishing these two paintings as bolt mates. This further reinforces Liedtke’s claim that these two paintings were intended by Vermeer as a pendant pair.
Thread Counting
The first step in ascertaining if two separate canvases were previously bolt mates is to check for a match in the average thread counts. Without “matching” counts, typically considered to be within 1 thread/cm of each other in the warp direction, they cannot be bolt mates. But an average thread count match alone is insufficient to establish bolt-mate status.4 This is particularly perplexing for Vermeer because such a large fraction of his canvases have average thread counts near 14 th/cm.5
Claims have been made, prior to the advent of software for automated thread counting and the computer calculation of weave maps, regarding bolt-mate status based on similar average thread counts in conjunction with close observation of canvas texture. The texture of the canvas may be described in terms of the frequency of irregularities in the weave such as groupings of thick and thin threads
[T]he Rolin painting [Young Woman Seated at a Virginal] is small, but with a rather coarse weave. A painting of a similar size, the Lacemaker . . . is on a canvas made of precisely the same type of rather coarse fibre and has exactly the same thread count. . . . Both canvases can be compared in raking light and in X-ray, where a series of irregularities can be seen, particularly in the vertical threads. . . . The canvas of the Lacemaker has just the same type of irregularities. So similar is the appearance of the two canvases that they could well be from the same bolt of cloth.6
This claim was subsequently supported by a computer-generated weave density pattern match.7 Such observed similarities in the canvas weave density pattern frozen at the time of priming and ground layer application put the matching canvases in physical proximity at some point in their histories. Combining this with other forensic data and knowledge of an artist’s studio practice can offer insight into authenticity, dating, and even the artist’s intent, e.g., regarding pendant pairs.
To imagine the appearance of a weave map, where the thread count within each small square evaluation tile is represented by an assigned color, consider the weaving process. The threads that run through the long dimension of the woven bolt of fabric are labeled the warp threads. These threads are wound around a beam and run tautly through the loom to be wound up on the cloth beam. In between, they are threaded through slits in the reed designed to help achieve a particular overall thread count (in threads/cm) across the width of the woven fabric. However, their placement and, thus the spacing between threads, has some flexibility so that each group of a few adjacent threads can have a modestly different number of threads/cm when measured across the width of the fabric.
The weft threads, which are shuttled back and forth across the width of the fabric, are packed by the weaver with the closure of the beater bar that is parallel to the weft threads.8 For each crossing pass of a weft thread, the weaver raises and lowers different harnesses containing treadles through which the warp threads travel on their path through the reed. The treadles raise and lower different subsets of the warp threads to implement the interwoven nature of the fabric. Vermeer’s canvases exhibit a simple weave with a one-over, one-under pattern as the weft thread traverses the warp threads. The adjacent weft thread follows the one-over-one-under pattern but with the warp threads switched as to which one is above and which is below.9 While the straightness of the weft threads as they traverse the fabric is maintained by the beater bar, their local spacing depends on the force with which the weaver presses the beater bar against the already-woven portion of the fabric. Indeed, due to unavoidable variations in the force applied in pressing the beater bar against the already-woven fabric, the local density in threads/cm of the weft threads can be expected to vary more as one moves along the warp direction of the fabric than the local density of the warp threads varies as one moves along the weft direction of the fabric.
Due to the weaving process, a group of several adjacent threads in either direction can be expected to vary less in density (as measured in threads/cm) as they travel through the fabric than the adjacent groups of threads crossing the fabric in the same direction. This is what causes the characteristic “stripes” in the weave maps. This effect was anticipated, prior to the advent of automated thread counting, with the admonition to avoid counting in spots along the same threads, thus removing a potential source of bias in the calculation of the average density.10
Now, imagine a color-coded image of the thread counts in either thread direction. In many cases, the dominant feature is a collection of stripes running across the image in the direction of the threads being counted. Because such an exhaustive counting at all spots across a painting’s canvas was deemed infeasible to accomplish manually, the resulting stripes were never fully visualized in the painting canvas support analysis literature prior to the advent of automated thread counting. However, at the first public presentation of such a weave map,11 the audience reaction was one of immediate recognition that the striped pattern, which continues through the original bolt, could serve as a “fingerprint” for canvases cut from the same bolt of canvas.

A quick, crude method for counting threads uses a grid superimposed on a magnified X-radiograph, such as in fig, 1. The patch in fig. 1 is a 2 x 2 cm square from an X-radiograph of The Milkmaid with a grid of 0.5 cm squares. There are approximately 28 vertical threads at the top edge of the square for a density of 14 th/cm. The horizontal thread count along the right side of the 2 cm square is also approximately 28 for a density of 14 th/cm. Many more spots would need to be counted and included in the average before it becomes trustworthy, with 15 in each direction recommended by Ernst van de Wetering.12
Weave Density Maps
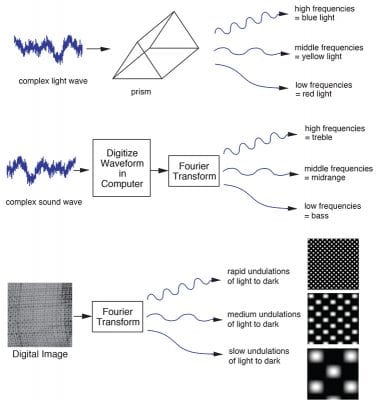
Such manual thread counting is laborious and is only undertaken on selected locations across the surface of a canvas. Several techniques have been applied in order to automate the counting procedure, including the use of the Fourier transform,13 autocorrelation,14 and thread-level analysis.15 The Fourier method pursued here decomposes a signal (such as an image, a light wave, or a sound) into a collection of frequency bands. This can be understood by analogy with a prism, which takes a light wave and breaks it into low frequencies (red light), middle frequencies (green light), and high frequencies (blue light), as shown in fig. 2. The analogous operation on sound waves decomposes a complex sound into low frequencies (bass), middle frequencies (mid-range), and high frequencies (treble). In applications, the signal (image, light, or sound) is decomposed into many hundreds of bands, and each band is associated with a coefficient that quantifies the signal strength in that portion of the total signal. The largest of these coefficients is the principal component, and in the thread-counting application, the principal component in the frequency range of interest is intimately related to the thread count.
With the introduction of such automated thread counting, it is possible to count everywhere across the canvas. A quick hand count, as in fig. 1, is used to set the frequency range of interest in the Fourier transform-based procedure. For The Geographer and The Astronomer, the patch size was a 0.75 cm square within which the local Fourier transform is computed. These evaluation tiles are distributed across the painting’s X-radiograph on a rectangular grid with their center points 0.25 cm apart. The location of the maximum peak in the Fourier transform in the region of interest set by the hand count is used as a proxy for the thread count. When the weave is sufficiently regular, as it is in the sample shown in fig. 1, this computed proxy is a good estimate of the manual thread count. In any event, the frequency of this principal component is a local feature of the canvas that can be compared to the same feature of a second canvas. For The Geographer, the horizontal thread density computed in this manner is 14.4 th/cm with a standard deviation of 1.2 th/cm, while the vertical density is 13.1 th/cm with a standard deviation of 0.9 th/cm. Similarly, the average thread count for The Astronomer is 15.6 th/cm with standard deviation 1.06 th/cm in the horizontal direction and 13.2 th/cm with standard deviation 0.86 th/cm in the vertical dimension. The computed vertical thread count averages are well within the typically accepted 1 th/cm threshold for warp threads, while the average counts for the horizontal threads differ by a bit more than 1 th/cm, which is acceptable for weft threads.16

To convert the similarity assessment into a visual task, the density values for each evaluation tile are transformed into colored squares at each evaluation spot. The resulting weave density maps for The Geographer and The Astronomer appear in fig. 3. The two maps shown indicate the densities of the vertical threads. The immediately obvious defining feature in each of the two maps is the pattern of stripes. The specific pattern revealed will depend on the size of the evaluation tiles. As this pattern is the result of the manufacturing process, it will be shared by bolt mates. Figure 3 has aligned the two weave maps, after rotating the bottom one of The Astronomer by 180◦.
Conclusion
Due to the similarity of the subjects of The Geographer and The Astronomer (and the distinctness of these subjects from Vermeer’s other paintings), the apparent use of the same model, the similar sizes of the two paintings, and their accepted dating as having been created in the same time frame, no Vermeer expert will be too surprised to learn that these two paintings are on canvas from the same bolt. The matching weave density maps introduced here of the patterns of the local densities of their vertical threads support this conclusion. This fourth weave match discovered among Vermeer’s thirty-four paintings on canvas17 can be used to support the claim by Walter Liedtke that The Geographer and The Astronomer were intended by Vermeer as a pendant pair.




